Let continue the serie of computation of mathematical constants that we started with Euler Number. This time our target is π, the famous “3.14” ratio between circumference and diameter of a circle.
Since out target is to compute one million digits in few minutes this post will use concept of code optimization.
Like e, π is irrational (it is not a ratio of 2 integer numbers) and transcendental (it is not a solution of a finite polynomial with integer coefficients). It is studied since the begin of history (probably also before) for practical reason and it is one of the mathematical entities with more anecdotes together with e and the golden ratio φ, so much that there are a lot of books about it.
During time, many approximation methods of π have been explored, both geometrical and arithmetical, many of them lead to very elegant computation formulas. Since 1500 there has been a sort of race to compute as many digits of π as possible.
A major break-through for the computation was the discover of Taylor series for arctan.
\[ \arctan(x) = x – \frac{x^3}{3} + \frac{x^5}{5} – \frac{x^7}{7} + \ldots \]
We recall that tangent, tan x, is the ratio sin x / cos x, so since sin π/4 = cos π/4 = 1/√2 we know that tan(π/4) = 1. Using its reverse arctan we have:
\[ \arctan(1) = \frac{\pi}{4} = 1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \ldots \]
Or
\[ \pi = 4 \arctan(1) = 4 – \frac{4}{3} + \frac{4}{5} – \frac{4}{7} + \ldots \]
This converge slowly but it is easy to find formulas with better performance. For example:
\[ \frac{\pi}{4} = \arctan \left( \frac{1}{2} \right) + \arctan \left(\frac{1}{3} \right) \]
That geometrically is easy to show:
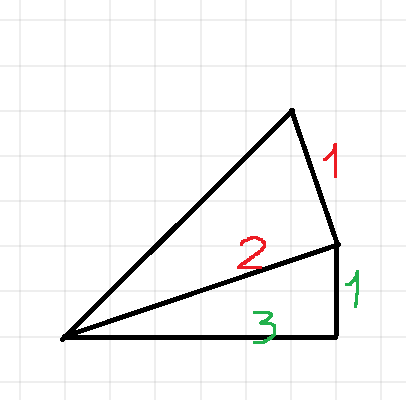
That leads to this formula, that thanks to powers of 1/2 and 1/3 converges much faster than the arctan(1) expansion.
\[ \begin{array}{rrl} \frac{\pi}{4} & = & \frac{1}{2} – \frac{1}{2^3 3} + \frac{1}{2^5 5} – \frac{1}{2^7 7} + \frac{1}{2^9 9} – \ldots \\ & + & \frac{1}{3} – \frac{1}{3^3 3} + \frac{1}{3^5 5} – \frac{1}{3^7 7} + \frac{1}{3^9 9} – \ldots \end{array} \]
In particular John Machin in 1706 used:
\[ \frac{\pi}{4} = 4 \arctan \left( \frac{1}{5} \right) – \arctan \left(\frac{1}{239} \right) \]
To compute 100 digits of π, but in 1700 and 1800 they managed to compute something like more than 700 digits with this method.
After WWII with the raise of computers the known digits increased fastly, reaching 1 million in 1973 always with this approach. Then scientists started using new methods, totally different, reaching 1 billion digits in 1989 up to 1014 digits in 2022. Please refer to Pi in Wikipedia for the whole history.
Implementation
We want to compute:
\[ \begin{array}{rrl} \pi & = & \frac{16}{5} – \frac{16}{5^3 3} + \frac{16}{5^5 5} – \frac{16}{5^7 7} + \frac{16}{5^9 9} – \ldots \\ & – & \frac{4}{239} + \frac{4}{239^3 3} – \frac{4}{239^5 5} + \frac{4}{239^7 7} – \frac{4}{239^9 9} + \ldots \end{array} \]
Let’s write a warm-up code with doubles and Java BigInteger like for e. Studying the terms, it is convenient to compute the fraction 1/5k in a variable and divide by the odd number in a separated variable, to recycle the 1/5k term for the next cycle (where we’ll need only to divide by 25). Idem for 239.
public static double binomialDouble() {
double pi = 0;
double fract5 = 16;
double fract239 = 4;
fract5 = 16.0/5;
fract239 = 4.0/239;
pi = fract5 - fract239;
for (int i=1; i<20; i++) {
fract5 /= 25;
if ((i&1)>0) {
pi -= fract5 / (i*2+1);
}
else {
pi += fract5 / (i*2+1);
}
fract239 /= 57121;
if ((i&1)>0) {
pi += fract239 / (i*2+1);
}
else {
pi -= fract239 / (i*2+1);
}
}
return pi;
}Ok, it works, let’s repeat it with BigInteger:
public static BigInteger binomialBig(int digits) {
String base = "000000000";
while (base.length()<digits+10) base = base + base;
if (base.length()>digits+10) base = base.substring(0, digits+10);
BigInteger pi = new BigInteger("0");
BigInteger fract5 = new BigInteger("16"+base);
BigInteger fract239 = new BigInteger("4"+base);
BigInteger term25 = new BigInteger("25");
BigInteger term57121 = new BigInteger("57121");
BigInteger termOdd;
int i = 1;
fract5 = fract5.divide(new BigInteger("5"));
fract239 = fract239.divide(new BigInteger("239"));
pi = fract5.subtract(fract239);
// 1 / 239^k will become zero faster thn 1/5^k
while (fract239.compareTo(BigInteger.ONE) > 0) {
fract239 = fract239.divide(term57121);
fract5 = fract5.divide(term25);
termOdd = new BigInteger(""+(2*i+1));
if ((i&1)>0) {
pi = pi.add(fract239.divide(termOdd));
pi = pi.subtract(fract5.divide(termOdd));
}
else {
pi = pi.add(fract5.divide(termOdd));
pi = pi.subtract(fract239.divide(termOdd));
}
i++;
}
while (fract5.compareTo(BigInteger.ONE) > 0) {
fract5 = fract5.divide(term25);
termOdd = new BigInteger(""+(2*i+1));
if ((i&1)>0) {
pi = pi.subtract(fract5.divide(termOdd));
}
else {
pi = pi.add(fract5.divide(termOdd));
}
i++;
}
return pi;
}Computing 10000 digits and comparing them in Internet it seams correct, so let’s see some timing.
| Digits | Time (sec) |
| 104 | 0.243 |
| 105 | 17.286 |
| 2 105 | 69.768 |
| 4 105 | 274.610 |
| 8 105 | 1095.024 |
| 106 | 1711.419 |
As for e, now we use long arrays having some attention on aggregate cycles and not considering zeroed parts. Here we had some surprise. 10000 digits were right, but computing 105 at some point (about 89500 digit) the result diverged. It was the variable “int i = 1;” that must be updated to “long i = 1;”, otherwise at i=18797 gave (2*i+1)*239*239 > 231, breaking the computation.
Good, but computing 400000 digits about at 384500 digits the result diverged again, because since we are using BASE 109, for i=80831 (2*i+1)*239*239 *BASE > 263 again breaking the computation, so we have to split in two the division by (2*i+1) and 2392.
You can find the final code in the git and here the comparison with BigInteger implementation (that can not “aggregate cycles”). As shown in the below table we already are faster than it.
It’s C time, let’s compare the code with not optimization flag during compilation and with -O2 and -O3 flag:
| Digits | Java BigInteger | Java arrays | C | C -O2 | C -O3 |
| 104 | 0.243 | 0.202 | 0.185 | 0.097 | 0.097 |
| 105 | 17.286 | 11.276 | 18.563 | 9.838 | 9.752 |
| 2 105 | 69.768 | 46.740 | 75.945 | 39.836 | 39.907 |
| 4 105 | 274.610 | 176.470 | |||
| 8 105 | 1095.024 | 757.923 | |||
| 106 | 1711.419 | 1128.562 | 1024.216 | 988.385 |
At this point a possible improvement would to parallelize the two arctan computations, but please note that arctan 1/239 converges faster and at the end the time would be dominated by the arctan 1/5, remaining something like 70-80% of the original time. We also could vectorize the code. All this fine tuning maybe will divide by half the execution time, but here the problem is that the arctan 1/5 converges too slowly, we need a faster converging formula.
In Wikipedia it is reported for example this one:
\[ \frac{\pi}{4} = 44 \arctan \left( \frac{1}{57} \right) + 7 \arctan \left( \frac{1}{239} \right) – 12 \arctan \left(\frac{1}{682} \right) + 24 \arctan \left( \frac{1}{12943} \right) \]
Putting it in code we get 105 digits in 7.62 sec. and 106 digits in 770.641 seconds. I expected a better improvement but 23% better is not bad, and in this case parallelization of computation of arctan could give a good improvement.
Conclusions
This computation as a sort of sentimental value for me. As far back as 2004 I placed 6th in the provincial phase of Mathematical Olympiads with a score that would have guarantee the access to national phase in any province but not mine, that was a sort of iron ring. There was an awards ceremony for the first ten placed in the province and I received some book, one of this was about Pi history.
There I found interesting anecdotes and algorithms, and since in that period I was learning C I started experimenting a lot of them and searching new ones in Internet. The following year with such a training I placed 31st on national Informatics Olympiads. I have been deeply changed by that experience, I understood that Informatics and Mathematics were my fields and I got a lot of self-confidence because I was very good in something so beautiful.
The e and π computations had been two my targets back in that times and I remember I obtained 1 million digits of e in 20 minutes and 100.000 digits of π in 15 minutes. I had a AMD K7 1.8GHz at that time, now I have an Intel i7 with 4 core at 2.50GHz, these programs are mainly single-cored so about 40% of speed improvement can be attributed to hardware.
For π I pass from 15 minutes to 7.7 seconds for 100.000 digits, so I guess I learned something along the road and now I get 1 million digits in less than 13 minutes (at that time I avoided them since they would have required more than 1 full day). The fact that for the million digits of e I only go from 20 minutes to 3 minutes (probably 6 on the same hardware) make me think that I knew what I was doing.. 🙂
I close this sentimental parenthesis and I let you one million digits of pi and the git with the code, with the hope of trying it again with a more efficient formula or more efficient implementation maybe to reach 10 millions or 100 millions digits.
One million digits Pi: download
Programs to compute Pi: https://github.com/zagonico86/my-snippets/blob/main/math-constants/pi/README.md